
Introduction
Harbor oscillations are motions of the water body originated by waves with long period. Oscillations may significantly interfere with harbor activities, disrupt them and create damage. For this reason they need to be carefully studied. Usually there is local awareness of the exposure of a site to harbor oscillations but the intrinsic behaviour of the phenomena also depend on the geometry of the harbor and therefore oscillations are to be carefully considered and evaluated in the design phase.
The technical term "oscillations" refer to waves whose behaviour do not change in space (they are also called stationary waves or standing waves), that are originated by the reflection of incoming waves by harbor walls (see Figure 1), which depends on the shape of the harbor, bottom friction and others. The reflected wave overlaps with the incoming wave possibly generating amplification. The typical wave periods that may generate oscillation range between 30 sec and 10 min. Vertical motions are generally limited, but wave length can be large. Contrary to what happens in open sea, waves are influenced by boundary conditions determined by basin size, shape, and also water depth.

Oscillations are caused by the resonance between wave period and the harbor characteristic period. The phenomenon is also referred to as harbor resonance, surging, seiching, and resonant oscillations. Incoming waves can be strongly amplified if the period is close to the harbor resonance period, therefore originating seiches. These are resonant (or near-resonant) standing oscillations in a semi-enclosed water body. In the Japanese literature they are commonly known as ‘secondary oscillations (undulations) of tides’.
Seiches
The term ‘seiches’ may derive from the Latin siccus, which means dry or exposed (from the exposure of the littoral zone at waves). Free-surface oscillations, known as seiches or seiching in lakes and harbours or storage tanks, have been noted and described already a long time ago; an episode of seiching in Lake Constance, Switzerland, was reported in 1549, and a record of observed seiches was taken in 1730 in Lake Geneva (Wilson, 1972; Miles, 1974). Korgen (1995) describes seiches as
the rhythmic, rocking motions that water bodies undergo after they have been disturbed and then sway back-and-forth as gravity and friction gradually restore them to their original, undisturbed conditions”.
Oscillation in ports can be accompanied by large horizontal motions (harbor currents). The horizontal motion mainly occurs where the vertical movement is limited. Tsunamis constitute another important problem: catastrophic destruction may occur when the frequencies of arriving tsunami waves match the resonant frequencies of the harbor or bay. This video shows how a tsunami can develop.
Seiches may occur in lakes, canals, bays and also along open seacoasts in particular situations. Lake seiches may be the result of a sudden change, or a series of intermittent changes in atmospheric pressure or wind velocity. Lake seiches are discussed here, here and here.
Seiches in canals may be triggered by adding or withdrawing large volumes of water suddenly. In bays, they can be originated by swells entering from the open ocean through the mouth of the bay, or changes in atmospheric pressure. Open ocean seiches may be originated by changes in atmospheric pressure, tsunamis of winds. A necessary condition is the similarity between the period of the forcing and the natural period of the water body.
Harbor oscillations differ from seiches in closed water bodies (for example, in lakes) for three main features (Rabinovich, 2010):
- they are mainly generated by long waves entering through the open boundary (harbor entrance) from the open sea;
- Harbor oscillations have a specific fundamental mode, the Helmholtz mode, similar to the fundamental tone of an acoustic resonator. This modes is absent in closed basins;
-
the decay of harbor oscillations is mainly due to radiation through the mouth of the harbor.
A basin may have several natural periods (also called ‘eigen periods’), which are determined by the basin geometry and depth. In natural basins these periods may vary from a few tens of seconds to several hours. The oscillations are known as natural (or eigen) modes. The mode with the lowest frequency (and thus, the longest period) is referred to as the fundamental mode. An interesting view of seiches induced in a laboratory tank is shown in this video.
As pointed out above, harbor oscillations can be a significant problem for inner harbor components and moored vessels within a harbor basin. Resonant periods characteristic of moored vessels often fall into the same range of periods as harbor oscillations thus possibly generating further resonance. Therefore, oscillations can produce damaging surging, yawing and swaying of ships at berth in a harbor. They can create dangerous mooring conditions including breaking of mooring lines, damage to fender systems, vessel collisions, and delays of loading and unloading operations at port facilities.
Analytical treatment of the phenomena is only possible for simple configurations of the harbor and forcing. Complex geometries or forcings are analysed by applying numerical models. In what follows, we will consider the simple case of an open basin with regular and rectangular shape.
Definitions
Regarding the geometry of the harbor basins, we distinguish between:
- Closed basin - a basin that is not in communication with a larger water body. An example of a closed basin is a lake, or a canal.
- Open basin - a basin that is in communication with a larger water body along at least part of one side. An example is the harbor.
Regarding forcing, we distinguish between:
- Free oscillations - oscillations that occur without external forcing (although some external forcing was applied earlier to initiate the oscillations).
- Forced oscillations - oscillations in response to external forcing.
Forced oscillations and free oscillations may combine. For example, seiches are originated as forced oscillations, but then they may continue for a long time as free oscillations. The set of seiche periods and associated seiche structures are a property of the harbor basin and are independent of the external mechanism forcing the oscillations. On the other hand, the amplitudes of the generated seiches strongly depend on the energy source that generates them, thereby exhibiting large variability.
We also identify the problem as:
- 2-dimensional - oscillations are independent of one horizontal dimension.
- 3-dimensional - oscillations vary in both horizontal dimensions.
Note that some textbooks refer to the one-dimensional approach by adopting the same definition given above for the 2-dimensional problem.
Hydrodynamics of seiches
The theory of oscillations is similar to the theory of free and forced oscillations of mechanical, electrical, and acoustical systems. A pendulum is a typical example. If perturbed, it continues to oscillate at its natural frequency, until friction tend to dissipate energy and the amplitude of oscillations decays exponentially. In the case of a periodic continuous forcing, forced oscillations are produced with amplitudes depending on friction and the proximity of the forcing frequency to the natural frequency of the system. In resonance, the amplitude of the oscillations may continue to increase until the energy that is intermittently added is equal to the energy that is dissipated.
To understand how standing waves and seiches form, let us recall the dynamics of water wave reflection, which happens when an incoming wave into a harbor meets the harbor head, which is usually marked by a wall. The problem is discussed here.
Let us assume that the harbor has rectangular shape and constant depth, the head is delimited by a vertical wall and that the wave crest is aligned with the direction of the wall, so that the wave dynamics is 2-dimensional and the wave is reflected perpendicularly and with full reflection.
Let us also assume that there is no damping of waves along the basin. In such circumstances, the wave is reflected with the same phase but opposite direction and approximately the same amplitude as the incident wave. This configuration satisfies the necessary boundary condition that the horizontal velocity is always zero. The resulting wave pattern is shown in Figure 2, 3, 4, 5, 6 and 7 and leads to to a standing wave.
An example of formation of a standing wave for different frequencies is shown in this video. Possible frequencies for a standig wave are explained in this video.
In mathematical terms, the analytical description of the resulting wave pattern after reflection \(w_s\) is obtained by superimposing the incident \(w_i\) and the reflected \(w_r\) waves depending on the coordinates x and t, namely,
\(w_s(x,t)=w_i(x,t)+w_r(x,t)\)
where
\(w_i(x,t)=\frac{H_i}{2}\cos\left(2\pi\left(\frac{x}{L}-\frac{t}{T}\right)\right)\), (1)
\(w_r(x,t)=\frac{H_r}{2}\cos\left(2\pi\left(\frac{x}{L}+\frac{t}{T}\right)\right)\). (2)
Here, \(H_i\) and \(H_r\) are heights of the incidente and reflected waves, respectively, \(T\) is period and \(L\) is the longitudinal length of the harbor.
Let's assume that \(H_i=H_r=H_s/2\). Then,
\(w_s(x,t)=H_s\cos\left(\frac{2\pi x}{L}\right)\cos\left(\frac{2\pi t}{T}\right)\)
Eq. (1) and (2) highlight that the incident wave is reflected by a wall by keeping the same phase and amplitude. Given that waves are travelling along opposite directions - and withouht any change in phase - the superimposition of the two waves results in a wave with an amplitude that is given by the sum of incident and reflected amplitudes.
The points there is no vertical movement with time are termed as "nodes". By contrast, at the antinodes, crests and troughs appear alternately. At the antinodes. Water motions at the seiche nodes are entirely horizontal, while at the antinodes they are entirely vertical.
The resulting configuration at time \(t=0\) and \(t=T/2\) is depicted in Figure 2.

Figure2. Resonance between an incident reflective wave and a reflected wave. At the nodes, the amplitudes of both waves cancel each other out, resulting in that the amplitude of the total wave is zero. At antinodes, the amplitudes of the incident wave and the reflected wave enhance each other. Modified after HinnevdZant, CC BY-SA 4.0 <https://creativecommons.org/licenses/by-sa/4.0>, via Wikimedia Commons.
Figure 3. A diagram of what happens to a transverse wave when it hits a free boundary: it reflects such that it does not invert (phase is not changed). This means that every incident crest returns as a reflected crest. Self-created. CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=96570
Figure 4. A diagram of what happens to a transverse wave when it hits a fixed boundary: it reflects such that the phase is inverted (that is, every incident crest becomes a reflected trough). Self-created. CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=96567

Figure 5. Superimposition of an incoming wave and a wave reflected by a harbor head with full reflection, with a node on the left boundary and an antinode at the right boundary. The mouth of the harbor on the left and the head on the right. Modified after Lookangmany, Wolfgang Christian and Francisco Esquembre - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=39309437
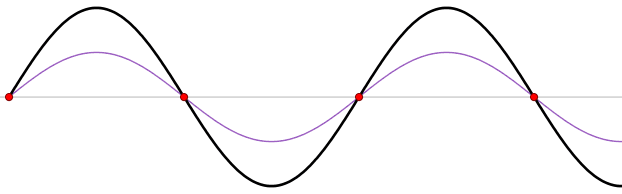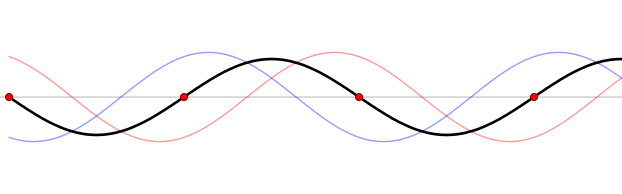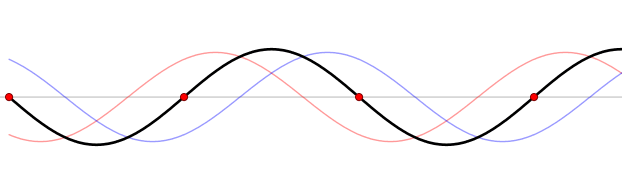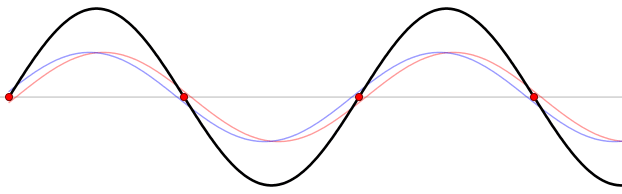
Figure 6. Wave reflection by a harbor head. Nodes are marked by red circles. Modified after Lucas Vieira - Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=535974
What happens in the harbour is the same process that we can observe when a wave propagates along a string with a fixed end on the left and a free end on the right. At the fixed end there is a reversal of phase and we find a node, while an antinode is found at the free end where there is no phase change (see Figure 7). Since at the free end the reflected and incident wave add to each other while moving in opposite directions, the appearance of propagation is lost and the resulting vibration is called a standing wave.

Figure 7. Standing waves along a string with fixed end and free end.
In open basins, we observe an antinode at the harbor head because water is free to move up and down the wall. Conversely, at the harbor mouth the inversion of phase originate a node. In closed basins, we observe an antinode at both ends. With no damping, the standing wave perpetuates as we can see in in this video.
Actually, in real harbors the node at the mouth is not precisely located at the mouth itself. In fact, radiation into the open sea causes the node to be located closed but outside the mouth. In analytical computation, we then introduce the "mouth correction".
Simulation of a standing wave can be easily obtained in the PC. With the R software, you may want to cut and paste this code. The transitory leading to wave formation is an approximation of what happens as there is not any smoothing from the calm to the disturbed conditions. Also, the code just superimposes the incoming and reflected wave geometrically. No energy losses are considered and no amplification is reproduced beyond the summation of the amplitudes of the incoming and reflected wave.
Resonance
Resonance occurs when the frequency of the incoming wave matches (or is closed) to the natural frequency of the harbor. In these conditions, the energy of standing wave is continuously increasing leading to amplification of its amplitude. Amplification depends on the frequency of the forcing, with the lowest modes of oscillation being more dangerous. It also depends on harbor length, depth, friction and others, as mentioned above.
Resonance is a matter of concern for several infrastructures. An example is the collapse of the Tacoma Narrow Bridge in 1940 (see Wikipedia and this video).
As aforementioned, free oscillations occur at the natural frequency of the system if the system is in state that is not in equilibrium. Without additional forcing, these free oscillations retain the same frequencies but their amplitudes decay exponentially due to friction, until the system eventually comes to rest. This is the case of standing waves, if the incoming wave ceases. In the case of a periodic continuous forcing, forced oscillations are produced with increasing amplitude depending on friction and the proximity of the forcing frequency to the natural frequency of the system.
The mathematical description of resonance requires the application of a dynamic model based on conservation equations, that takes into account friction and radiation into the open sea of the reflected wave. Here, we limit our analysis to the estimation of the natural period of the harbor. As we said, this is the first step to check whether there are the conditions for resonance.
Merian (1828) proposed a formula to estimate the natural period for closed and open rectangular basins with length \(L\) and depth \(D\) (which, as noted above, is supposed to be constant along the basin itself), under the assumption of absence of friction. Merian's formula for closed basins reads as:
\(T_n=\frac{1}{n}\frac{2L}{\sqrt{gD}}\) (3)
where \(g\) is gravity and \(n\) is the number of nodes. The basin is characterised by a fundamental mode of oscillation, with only one node, and other modes corresponding to increasing number of nodes (see Figure 6). The modes with increasing number of nodes are less dangerous with respect to the fundamental mode, for the increasing effect of friction and dumping.
Figure 8. Oscillation modes for closed and open basins. From Sabatier F. (2007). After Carr (1952).
For open basins, we need to impose the presence of a node at the open end (Figure 7) and therefore Merian's formula reads as:
\(T_n=\frac{1}{1+2n}\frac{4L}{\sqrt{gD}}\) (4)
The period for the fundamental node (n=1) is
\(T_1=\frac{4L}{\sqrt{gD}}\). (5)
The Merian's formula allows a quick and easy estimation of the period of a bay. It can be used to derive initial trial values to be compared with the forcing period to detect possible hotspots, to be further inspected through numerical simulation. Thorade (1931) found that Merian's estimate should be increased by 10% if the width of the bay is about 1/10 of its length. If the width is comparable to the length, than the estimate should be increased by 32%. In general, Merian's formula overestimates the period with respect to more precise computations.
For example, the estimate of the first mode for the Lake Superior (USA) provided by Meriam's formula is about 9.45 hours, while numerical computation yields 7.19 hours. For the Lake Michigan, Merian's estimate is 10.53 hours against a numerical estimate of 8.83 hours.
References
Carr, J. H. (1952). “Wave Protection Aspects of Harbor Design,” Report E-11, Hydrodynamics Laboratory, California Institute of Technology.
Korgen, B.J., 1995: Seiches, American Scientist, 83, 330-341.
Merian, J. R. (1828). über die bewegung tropfbarer Flüssigkeiten in Gefässen. Schweighauser.
Miles, J.W., 1974: Harbor seiching, Ann. Rev. Fluid Mech., 6, 17-36.
Thorade, H. (1931). Probleme der Wasserwellen.
Wilson, B., 1972: Seiches, Advances in Hydrosciences, 8, 1-94.
Rabinovich, A. B. (2010). Seiches and harbor oscillations. In Handbook of coastal and ocean engineering (pp. 193-236).
Sabatier, F. (2007). US Army Corps of Engineers, Coastal Engineering Manual (CEM), Engineer Manual 1110-2-1100. US Army Corps of Engineers, Washington, DC (6 volumes). Méditerranée. Revue géographique des pays méditerranéens/Journal of Mediterranean geography, (108), 146.
Download the powerpoint presentation of this lecture
Last modified on March 8, 2023
- 327 views
